Democracy without elections

Tech Breakfast

Dr. Andreas Maier

2023-10-05

Introduction

For more than two thousand years, until the 18th century, democracy was seen as the rule of the people, when political institutions emerge directly from the people largely by lot(tery).

  • The process to select government officials by lot is called sortition.
  • Alternative name for government using sortition: demarchy.

Ancient Athens

Es gilt z. B. für demokratisch, daß die Staatsämter durchs Los, für oligarchisch, daß sie durch Wahl besetzt werden“

– Aristoteles: Πολιτικά (Politik), 345 bis 325 v. Chr.

Eligible for public offices:

  • all 30 year old male
  • no women, no slaves, no foreigners
  • in total 10% of athens population (30-40000)

Deputies, judges and most senior officals were determined by lot.

  • Assembly of 6000 drawn by lot
  • Council of 500 drawn by lot (prepares assembly and participates in government)

The random distribution of this office was an essential pillar of democracy:

I judge my neighbour and he judges me.

– Franziska Weise

Kleroterion

Kleroterion usage

N rows and M columns of slots (e.g. N=50, M=5 (but also M=11))

  1. Wooden cards with names are distributed randomly on the slots (Other description: one column per tribe/party/family)
  2. A number P of people to be elected is chosen
  3. N balls/dices are used for the selection
  4. P/M white balls/dices and N - P/M black balls/dices are mixed
  5. The balls/dices fall in random order into a tube.
  6. If a white ball falls out of the tube the top row is selected (the cards get removed and the owner gets called forward), if a black ball falls out of the tube top row is discarded (the cards get removed)

The first significant examination of Athenian allotment procedures was Headlam-Morley (1891): On Election by Lot at Athens

Florence 1300 - 1500

General mistrust against too powerful persons and groups

  • Officials are selected by lot each year among 2000 citizens recognised as suitable for office
  • Participation allowed only every 3 years
  • Consecutive terms were forbidden
  • Eligibility was checked every five years (no tax debts, membership in guilds, …)

This method was also adopted in Orvieto, Siena, Pistoia, Perugia and Lucca

This lottery procedure “is more likely to promote good life, sound administration and government in the towns and cities than the orders which, conversely, are based on election. They are more united and equal, more peaceful and free from passions”.

– King Ferdiand II

Age of Enlightenment

“The suffrage by lot is natural to democracy; as that by choice is to aristocracy.” „Die Entscheidung durch das Los entspricht dem Wesen der Demokratie, die Entscheidung durch Wahl dem der Aristokratie.“

–- Baron de Montesquieu: De l’esprit des loix (Vom Geist der Gesetze), 1748

But:

  • Wealthy enlightenment figures preferred to retain more power by holding election
  • They simply dislodged a hereditary aristocracy to replace it with an elected aristocracy

French Revolution: Hereditary nobility replaced by elected nobility

French Republic, not French Democracy!

Optimal sample size

Democracy is possible only if the decision-makers are a representative sample of the people concerned.

– John Burnheim (1985): Is Democracy Possible?

If you have cooked a large pan of soup, you do not need to eat it all to find out if it needs more seasoning. You can just taste a spoonful, provided you have given it a good stir.

– George Gallup

How many samples \(n\) from a total of \(N\) items do we need, so that our sample is representative?

Sample size formula

The formula for computing the sample size \(n\) of a finite population \(N\) \[ n = \frac{n_\infty}{1 + \frac{n_\infty - 1}{N}} \] where the sample size for an infinite population \(n_\infty\) is given as \[ n_\infty = \frac{z^2 p(1-p)}{e^2} \] with the the z-score \(z\) for a specific confidence level, the margin of error \(e\) of your sampling results and \(p\) being the proportion of the population picking a specific choice (\(p=50%\) generates maximal sample sizes).

Sample size formula 2

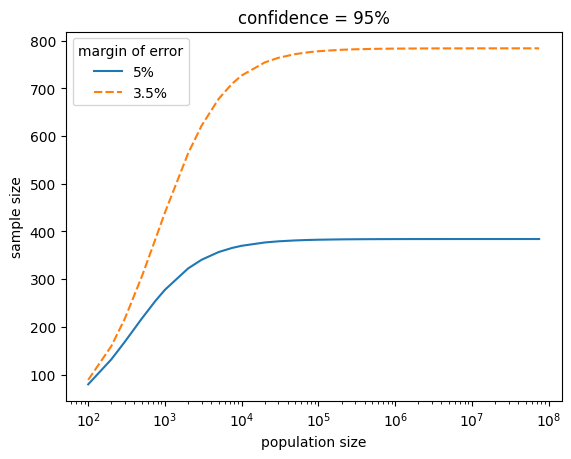
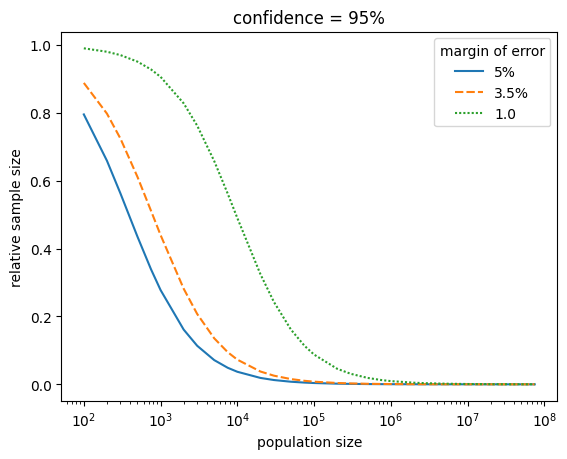
Sample sizes table

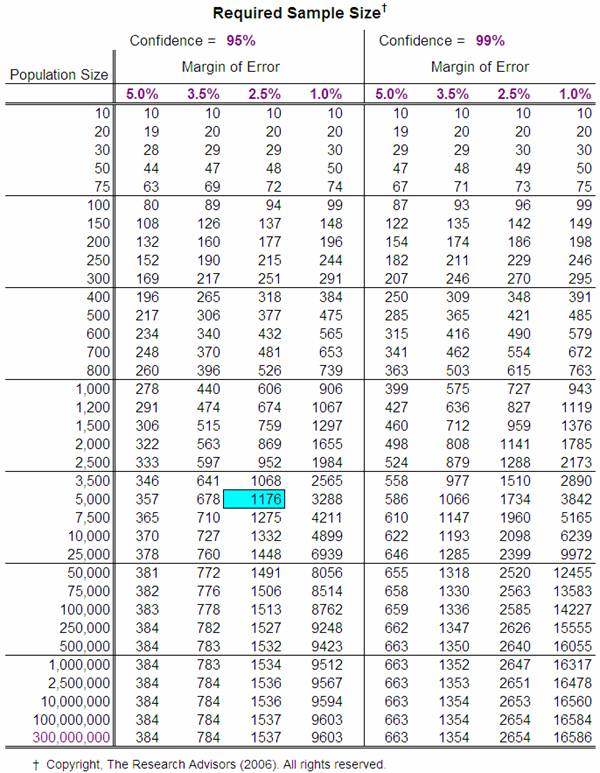
Sample size examples

If you want to be confident that in 95% of the decisions the parliament represents the will of the people within an error margin of 5%, the sample size formula suggest a parliament size of 384 people (for a population > 1 million)

If the European Parliament with 751 seats would be selected by lot in 95% of the cases the will of the european people would be represented with a margin of error of about 3.5 %.

For a village with 1000 persons, we need 440 in the “Gemeinderat” for the same margin of error.

=> Sortition/Selection by lot is much more efficient for bigger population sizes

Modern examples

Citizens’ Assembly on Electoral Reform (Canada, 2004)

  • 160 persons selected by lot (stratified)
  • followed by referendum (failed)

Constitutional reform (Iceland 2010- 2013)

  • 1000 persons selected by lot
  • 25 elected from 1000 to create new constitution
  • followed by referendum (result not accepted by parliament)

Convention on Constitution (Ireland 2013)

  • 66 persons selected by lot ((stratified) + 33 politicians
  • followed by referendum (successful)

Bürgerrat (Germany 2019 - )

  • 160 persons selected by lot (stratified)
  • Only recommendations

Jury trials (USA and many others…)

Advantages

  • neutral, fair, representative (secured by statistics, not by quotas)
  • cheap, no expensive campaigns necessary
  • difficult to manipulate
  • no professional politicians, no long-term corruption

Disadvantages

  • Expert burocrats might have a lot of power and manipulate layman politician
  • laymen politician might use their short time in power to get rich as fast as possible
    • Lobbyists might have it even easier with laymen
  • no longterm planning and stability, because probability of same person again selected is only (80 Million/800 = 1/100000)

Mixed election/sortition models

  • One chamber elected, one chamber selected by lot
  • Proportion of non-voters represented by people selected by lot
  • political conscription -> If you are selected you have to serve (like military conscription)

References

Books

Links

Thank you

Contact me

Dr. Andreas Maier

Senior Data Scientist

andreas.maier@um-orange.com